この前は、指数関数が虚数を挿入することによって、波の世界に代わってしまうことを説明しました。
実は、虚数は虚構の世界の物とは断定できず、実世界を理解するのに、ひじょうに重要な概念なのかもしれない、ということです。
そこで、今日は、虚実混合の世界を表すもの、複素平面に関して説明します。
平面は東西方向と、南北方向に分けられます。東西方向は実の世界、つまり、実数を表します。実数とは、整数、有理数(分数)、無理数(ルート3など)の総称です。
南北方向は、虚数の世界です。2つ合わせて複素数と言います。また、このような座標を複素平面と呼びます。
少し話を変えますが、座標(住所)は基本的に横と縦の長さで決めますよね。例えば、「1条4丁目」のようにです。数学でも同じなんですが、場合によっては、原点からの距離と真東をゼロとして左回りの角度で表すこともあります。
ここで、数学では角度を円周の比で表します。何で?とお思いでしょうが、長さに関連させるのに便利という理由からです。
学校で習った円周は、2πrでした。もし、半径が1ならば(これを単位円といいます)円周は2πです。つまり、1周(360度)を2πと表せます。(単位はラジアンといいます。)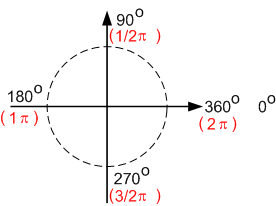
図を見ればわかりますが、180度は半周なので、πです。これさえ分かれば、30度でも120度でも、円周率で表現できます。
先ほども言ったように、南北は虚数を表し、東西は実数を表します。それぞれ独立していると考えていいでしょう。東西をx、南北をyとすると、座標は、 になります。
もし、上のように角度を使うと、座標は、 とも表現されます。
は、角度です。本当かどうか、試してみましょう。
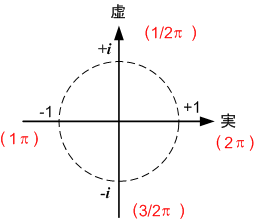
真東から90度(2分のπ)のところに+iがあります。上の式を使うと、になります。コサイン90度(または、
)はゼロになりますが、サイン90度は1になります。
したがって、になって、座標の値と一致しています。
前回のオイラーの公式を覚えていますか?ですね。つまり、指数関数だけでも複素平面の座標を表すことができるのです。
面白い世界ですね。では、また次回をお楽しみに。

