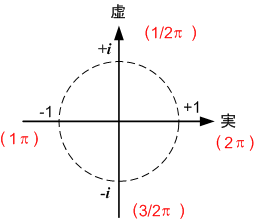
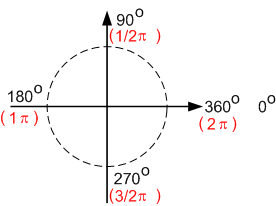
最近、アメリカのマサチューセッツ州の高校に留学中の日本の方に数学を教える機会がありました。
日本で言う微分積分の基礎に関する教科です。日本では、数Ⅱ、数Ⅲと言われるものでしょう。
10年以上高校で教えている教科に関しては、全く触れていなかったので久しぶりにアメリカと日本の微積分の教科書を比べてみました。
(ちなみに、マサチューセッツは比較的教育レベルが高く、州だけでいえば、世界でも上位に来るくらいです。)
私は、以前から日本の高校数学のカリキュラムは中途半端だと申しています。今回、アメリカの教科書を見て、より良く認識できました。
アメリカの教科書は、大学で取る微積分の講義が分かるような基礎を全体にわたって教えている感じです。
一方で、日本の場合は、明らかに大学入試を作成するのに問題が起こらないように、教える範囲を制限しているように見えました。
日本の良いところは、このようなカリキュラムでも上から言われたことは、文句を言わず真面目に教えるところでしょうね。(少し皮肉っぽいですが)
逆にアメリカは、良いカリキュラムなのに、きちんと教えられる教師が少ないというのが問題のようです。
世の中では、「教育を良くしよう」とか安易なことを言いますが、それほど簡単ではないようですね。