大人のための家庭教師　ブログ

物が回れば、中に入っているものが遠心力を受ける、という表現は、間違ってはいないのですが、遠心力というものが独立して存在するというのは、違います。

「車を運転して、ハンドルを右に切れば、左に体が引っ張られるじゃないか！」と言いますが、ハンドルを切る方向に力をかけたから、左に「見かけの力」が働いただけなのです。

つまり、遠心力も同じで、向心力（中心に引っ張る力）があるから、外側に離れていくような見かけの力（遠心力）が生じるということです。

このような話をすると、禅問答のように聞こえがちですよね。「あなたの言ってることは、わからないではないが、ピンとこねぇ」なんて声が聞こえそうです。。。

では、明快な例を示しましょう。糸の先に物体を付け、糸の先をもって回してみます。下の絵を見てください。

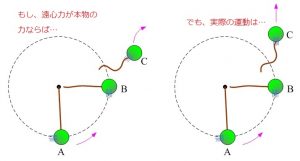
二つの絵がありますが、いずれもBの場所で糸を離しています。もし、遠心力が実在した力であれば、左の絵のように、離れた時点で、外側に物体が飛んでいくはずです。

しかし、現実は、右の絵のように円運動の接戦方向に飛んでいきます。つまり、遠心力というのは、そもそも物体には、かかっていないのです。

多少の混乱はあるでしょうが、「本物」の力と見かけの力の違いというのは、物理学を矛盾なく進めていくのに重要である、と覚えてもらえれば、うれしいです。

大人の家庭教師

補足：　ご指摘にもありましたように、ここでの説明は、あくまで初歩的なものになります。ですから、誤解を招くような表現もあるかもしれません。ただ、実際に、円運動をしている物体にかかっているのは、向心力だけです。そうでなければ、円運動を物理学的に記述できないのです。また、上の図例は、遠心力が独立して物体に働いていないことを示しているだけということも、ご了承ください。

現実には、遠心力などは非慣性系を考慮したときに出てくる力で、これを物理の用語で「見かけの力」（英語でfictitious force）と言います。もちろん、それらの力で説明できる現象などもあり、ここでは、すべてを解説していませんので、ご興味のある方は、正規の教科書を参照したり、授業を取ることをお勧めします。

身の回りで起こっていることを、数字にすると結構驚く事ってありますよね。

例えば、太陽の大きさは地球から見ると大したことがないですが、体積比で約地球の130万倍の大きさがあります。

その太陽が石炭のようなものでできているとしたら、約数千年で燃え尽きてしまいます。そんなに大きくても、それだけ勢い良く燃えていれば、すぐに燃え尽きてしまうのです。

「数千年でもすごい！」とお思いでしょうが、太陽の現在の年齢は約46億年と言いますから、数千年なんて太陽の人生にとっては一瞬の出来事です。

それでは、どうしてあれだけのエネルギーを、こんなに長い間出し続けられるのでしょうか？

実は太陽では核融合が起きて、エネルギーが放出されます。大きな太陽が生む重力が原子を狭いところに閉じ込められるために、実現できることなのです。

もう一つ、太陽がらみですが、地球と太陽の距離を想像できるでしょうか？「遠いようで近い、近いようで遠い」という感じでしょうか。まるで、お釈迦様の説教のようですが。。。

まじめな話をすると、光の速さ（電波の速さと同じ）で約500秒かかります。8分と20秒と言ったところです。中継で声だけが遅れて見えるという次元からほど遠い感じです。

これでもピンと来ませんか？では、地球の大きさをパチンコ玉くらいに縮小したとしたら、太陽までの距離はどれくらいになるか考えるといいかもしれません。

単純な比の計算、つまり、割り算をすると、100から200メートル先に太陽があるという計算になります。

結構離れてますね。常識的なものもありますが、知っているとちょっと自慢できる知識だと思います。

大人の家庭教師